随着互联网的飞速发展,个性化推荐已经成为各大网站、手机客户端的必备服务。如何持续优化、进一步提高推荐的精准度是一项复杂又令人兴奋的工程。
主流的推荐系统有协同过滤、基于内容的推荐、基于社交网络的推荐等。
很多推荐算法没有考虑到用户的短期兴趣,而用户的兴趣又是随着时间动态变化的,所以有效地捕获用户的兴趣偏好转换对提高推荐的准确性有着很大的辅助作用。
马尔可夫模型通过观察用户短期的行为数据,生成一个状态转移矩阵,根据该矩阵预测接下来一个时间点的用户行为,有效地利用了用户的短期兴趣偏好信息。
概念
安德雷·安德耶维齐·马尔可夫Андрей Андреевич Марков(1856.6.14-1922.7.20),俄国数学家。
1874年马尔可夫入圣彼得堡大学,师从切比雪夫,毕业后留校任教。
1886年当选为圣彼得堡科学院院士。马尔可夫的主要研究领域在概率和统计方面,他因提出马尔可夫链的概念而享有盛名。
马尔可夫链已经成功应用到物理、化学、语音识别、信息科学、金融等领域,谷歌所使用的网页排序算法就是由马尔可夫链定义的。
 安德雷·安德耶维齐·马尔可夫
安德雷·安德耶维齐·马尔可夫
马尔可夫过程
对于一个随机过程,如果其未来所处的状态仅与其当前状态有关,而与过去的状态无关,则该随机过程被称为马尔可夫过程。
马尔可夫链
假设马尔可夫过程 的参数集T是离散的时间集合,
则相应 取值集合空间是离散的状态集
设有随机过程 ,
若对于任意的整数 和任意
,
条件概率满足
则称 为马尔可夫链。
简单点就是说,时间和状态都是离散的马尔可夫过程即为马尔可夫链。
转移概率
为马尔可夫链 在时刻n的一步转移概率,其中
,简称为转移概率。
转移概率矩阵
设P表示一步转移概率 所组成的矩阵,且状态空间
,则
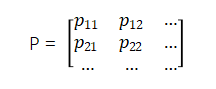
称为系统状态的一步转移概率矩阵,它具有的性质:
(1) ;
(2) .
n步转移概率、转移矩阵
为马尔可夫链 的n步转移概率,并称
为马尔可夫链的n步转移矩阵。
举个栗子
说到这里,可能还会有人问“随机过程是啥玩意儿”,“马尔可夫链到底是什么鬼”。
数学定义总是简单、精准、严谨,几乎没有逻辑漏洞,但可能不是特别容易理解,那么这个小节我们举几个栗子,更形象的解释下这些概念。
随机过程,就是一系列随机变量的集合。
比如,每丢一次硬币,便产生一个随机变量X,那么一次又一次的丢下去,便产生一系列的随机变量X1,X2,…,Xi,…。随机变量序列集合起来就是一个随机过程。
那么马尔可夫链又是什么呢?
它其实是随机过程的一种,具体是什么还是举个例子吧。
无忌是达观数据的员工,每天下午4点到5点有仨状态:吃水果(公司免费提供的、各种管饱)、写代码、技术交流,这就是传说中的状态分布。那么明天的这个时间段无忌会做什么呢?后天呢?大后天呢?假如他的状态转移是有概率的,比如今天吃水果,那么明天还吃水果的概率是0.3,写代码的概率是0.6,技术交流的概率是0.1。
直接看下表:
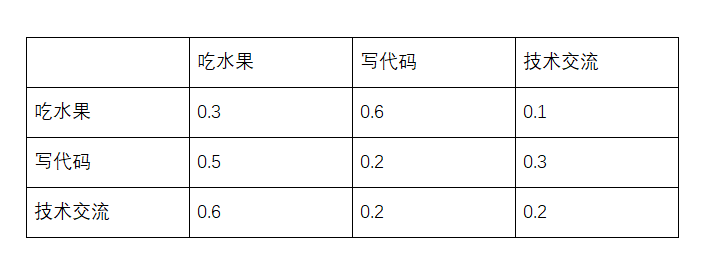 无忌的状态转移概率
无忌的状态转移概率
左边一列是今天的状态,上面一行是明天的状态。
图中的0.1表示的是无忌今天吃水果,第二天技术交流的概率。
这就构成了一阶转移概率矩阵。
这个例子中,无忌明天的状态仅仅与今天的状态有关,与过去无关,同时三种状态是离散的,构成了一个马尔可夫链。
推荐应用
用户行为分析
为了让推荐结果符合用户口味,我们需要深入了解用户。如何才能了解一个人呢?
《论语 · 公冶长》中,
“听其言,观其行。”
也就是说,可以通过用户留下的文字和行为了解用户的需求。
用户行为数据最简单的存在方式就是日志,用户的每次浏览、点击、购买、收藏等都记录在日志中,这些行为数据对于接下来的构建转移概率矩阵有着至关重要的作用。
假如在某购物网站中,对某物品的一次购买,称作一个状态。
某用户在 时刻购买了物品a,这里我们定义为状态{a};
在接下来时刻 该用户又购买了物品b和c,则由状态{a}转移到了状态{b}或{c};
这时在 时刻购买了d,状态转移到了{d},这样的话用戶不停的购买,状态也不停地转移。
形成了一条购买链,如图。
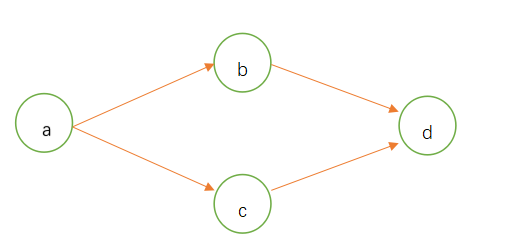 某用户的购买链
某用户的购买链
在这个例子中,我们仅仅讨论了针对单个用户如何构建购买链,对于所有用户来说,道理一样,只不过状态集扩大了而已。
转移矩阵的构建及使用
我们先讨论下非个性化马尔可夫模型,即假设每一个用户的转移矩阵是相同的,这样的话个性化推荐只能体现在将转移矩阵应用在用户的最后一次行为操作。
继续举个例子,通过对某段时间内所有用户行为进行分析,抽取出这些状态转移样本数据:(a,b,c)->(b,c)、(b,c)->(a,b),然后我们可以得到如下转移矩阵M:
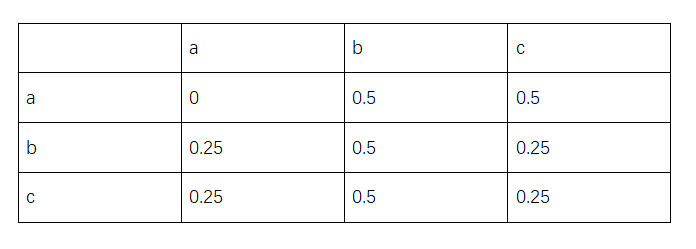 转移矩阵
转移矩阵
假如某个用户当前的操作物品是a、c,那么根据上面得出的转移矩阵,我们就可以计算出接下来该用户操作各个物品的程度,对这些结再进行标准化后就可以认为是接下来对各个物品进行操作的概率,
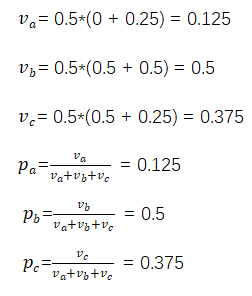 这个计算逻辑看起来可能不是特别容易理解,直接上公式,简洁明了!
这个计算逻辑看起来可能不是特别容易理解,直接上公式,简洁明了!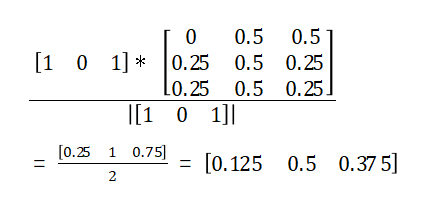 最后对
最后对![]()
进行标准化即可得到接下来对a、b、c的操作概率。
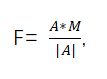 其中A是用户当前的行为矩阵,M为计算出来的转移矩阵,对结果F进行标准化后即可得到未来用户行为的概率预测矩阵。有了当前行为以及概率预测矩阵,我们就可以根据概率大小进行排序,优先推出概率大的物品,达到个性化的目的。
其中A是用户当前的行为矩阵,M为计算出来的转移矩阵,对结果F进行标准化后即可得到未来用户行为的概率预测矩阵。有了当前行为以及概率预测矩阵,我们就可以根据概率大小进行排序,优先推出概率大的物品,达到个性化的目的。
而对于个性化马尔可夫模型,可以怎么处理呢?
这里我们可以将对物品的偏好转化为对特征的偏好,假如某个物品的特征是「娱乐、影视」,那么对该物品的一次行为操作可以转化为对「娱乐」、「影视」的操作。
这样,通过对某个用户的历史行为日志进行挖掘分析,就可以得出用户在操作「娱乐」特征的情况下,下个时间段操作「影视」的概率,也就构成了用户的特征喜好状态转移矩阵。
这样的话,可以计算出每个用户的特征喜好状态转移矩阵,达到真正意义上的个性化。
多行为加权融合
上面提到的转移矩阵的计算是基于用户的某一种行为操作,即通过用户的单一行为来得到用户的偏好转换。
为了能更好的表示用户的喜好状态转换,可以通过多行为加权融合的方式来解决。
假如用户的行为操作有点击、购买、收藏、点赞,那么可以对每种行为类型计算出特征喜好状态转移矩阵,并得出用户在下个时刻的操作列表,也就是推荐列表,最后将多个推荐列表进行加权融合得出最终的列表结果。
多阶马尔科夫融合
考虑到用户操作行为的随机性,用户从状态s1到状态s5可能受到s2、s3或者其他因素的影响。并且在个性化推荐长尾现状的部分影响下,单个用户在极短时间内兴趣偏好不会发生太大变化。
这里可以通过采用多阶马尔可夫模型融合的方式进行对这种情况进行优化。比如一段时间内用户从状态s1到s2,再到s5,即s1->s2->s5,那么这次的状态转移记为s1->s5的二阶转移次数。
通过计算用户行为的多阶状态转移矩阵,基于相关矩阵得出预测列表,最后加权融合即可得到我们需要的推荐列表。
这里具体采用几阶模型,可以根据实际场景进行效果测试,阶数越高,预测的结果更大的基于用户长期的兴趣偏好,阶数约低,预测的结果更大的是基于用户短时间内的兴趣偏好。
总结
本文首先简单介绍了马尔可夫相关的数学概念,然后通过例子形象地解释了随机过程、马尔可夫、转移概率等实际含义。
在推荐系统的应用上,分析了如何通过用户操作记录进行构建状态转移矩阵以及转移矩阵的使用。
考虑到推荐的效果,我们又进一步介绍了多行为加权融合以及多阶马尔可夫融合的两个方案。
作者简介
张可,达观数据推荐算法工程师,负责达观数据个性化推荐引擎的研发、优化,以及推荐系统中机器学习算法的具体应用。一直在路上。