达观动态

达观数据在搜索引擎和推荐系统两个方面都有较深的功底，并且广受客户青睐！本文主要先简单介绍下推荐系统的流程框架，然后主要介绍下重排序。

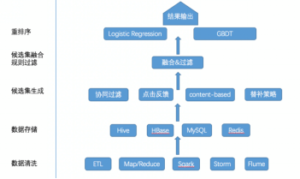
从框架上看，推荐系统流程可以分为数据清洗、数据存储、候选集生成、候选集融合规则过滤、重排序。

首先将客户上报过来的数据进行数据清洗，检查数据的一致性，处理无效值和缺失值等，去除脏数据，处理成格式化数据存储到不同类型的存储系统中。对于用户行为日志和推荐日志由于随时间积累会越来越大，一般存储在分布式文件系统（HDFS），即Hive表中，当需要的时候可以下载到本地进行离线分析。

对于物品信息一般存储在MySQL中，但是对于达观数据，越来越多的客户导致物品信息表（item_info）越来越大，所以同时也会保存在Hive表和HBase中，Hive可以方便离线分析时操作，但实时程序读取的时候Hive表的实时性较差，所以同时也会写一份放在HBase中供实时程序读取。对于各个程序模块生成的结果，有进程同步关系的程序一般会使用Redis作为缓冲存储，生产者会把信息写到redis中供消费者使用。候选集生成是从用户的历史行为、实时行为、利用各种策略和算法生成推荐的候选集。

同时点击反馈会根据用户的实时操作对候选集进行实时的调整，对于部分新用户和历史行为不太丰富的用户，由于候选集太小，需要一些替补策略进行补充。候选集融合规则过滤主要有两个功能，一是对生成的候选集进行融合，提高推荐策略的覆盖度和精度；另外还需根据产品、运营的角度确定一些人为的规则，过滤掉不符合条件的item，重排序主要是利用机器学习的模型对融合后的候选集进行重排序。

对于候选集生成和重排序两个层次，为了效果迭代需要频繁修改两层，因此需要支持ABTest。为了支持高效率的迭代，我们对候选集触发和重排序两层进行了解耦，这两层的结果是正交的，因此可以分别进行对比试验，不会相互影响。同时在每一层的内部，我们会根据用户将流量划分为多份，支持多个策略同时在线对比，来提高推荐效果。

对于不同算法触发出来的候选集，如果只是根据算法的历史效果决定算法产生的item的位置显得有些简单粗暴，同时，在每个算法的内部，不同item的顺序也只是简单的由一个或者几个因素决定，这些排序的方法只能用于第一步的初选过程，最终的排序结果需要借助机器学习的方法，使用相关的排序模型，综合多方面的因素来确定。

排序模型分为非线性模型和线性模型，非线性模型能较好的捕捉特征中的非线性关系，但训练和预测的代价相对线性模型要高一些，这也导致了非线性模型的更新周期相对要长。相较而言，线性模型对特征的处理要求比较高，需要凭借领域知识和经验人工对特征做一些先期处理，但因为线性模型简单，在训练和预测时效率较高。因此在更新周期上也可以做的更短，还可以结合业务做一些在线学习的尝试。

2.1 线性模型

线性模型主要介绍逻辑回归（Logistic Regression），逻辑回归是一种广义线性模型，虽然名字里带着回归，但它其实是一种分类算法，主要运用在二分类或多分类算法。在多分类中，有one-vs-rest(OvR)，和many-vs-many(MvM)两种不同的分类思路，这里主要讨论预测而分类问题（某个userid是否会点击某个itemid）。

首先将每个userid和每个itemid作为特征，模型函数为：

m,k分别为userid和itemid的个数， 分别为自变量 的参数。

逻辑回归模型采用极大似然法对模型的参数进行估计，Cost function为：

n为样本个数，为样本的label，用向量代替所有参数。然后是计算Cost function最大化时的参数。在最优化理论中，求解最优化参数有很多种方法，梯度下降、随即梯度下降、牛顿法、拟牛顿法，共轭梯度法，这里选用的是牛顿法。

牛顿法的思路很简单，就是把泰勒展式展开到二阶形式：

该式子成立当且仅当：

求解：

得出迭代公式：

牛顿法求根图示：

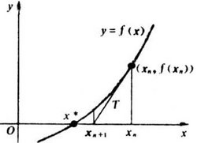
相比较而言，牛顿法比梯度下降法更容易收敛（迭代更少次数），但在高维情况下，牛顿迭代公式是：

其中H是hessian矩阵：

hessian矩阵增加了计算的复杂性，不过一般候选集数量都不会太多，所以还可以接受。

对于点击率预估而言，正负样本严重不均衡，所以需要对负例做一些采样。同时，在训练之前需要用TFIDF将训练数据转换为列向量，这样每一行是一个长度为m+k的列向量，再将结果作为模型输入训练。

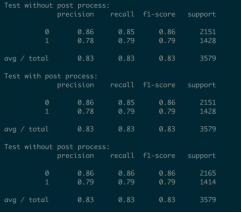
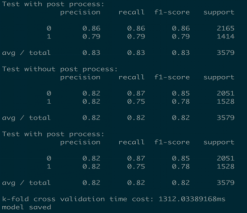
将候选集输入模型后，得到相应的预测概率，该概率就是将输入值转化为向量后，再用logit函数归一化道（0，1）之间的值，根据该值得到相应的顺序。

2.2 非线性模型

非线性模型主要介绍GBDT（Gradient Boost Decision Tree），以及相应的运用。GBDT是一种常用的非线性模型，是Boost算法的一种，先介绍一个称作AdaBoost的最流行的元算法。

Adaboost算法在开始的时候先为每个样本赋一个权重值，初始的时候，每个样本权重相同。每次迭代建立一个单层决策树分类器（可以用任意分类器作为弱分类器，只要它比随机猜测好略好就行不过弱分类器越简单越好），该分类器依据计算预测样本的最小错误率选出最佳单层决策树，同时增加分错的点的权重，减少分对的点的权重，这样使得某些点如果老是被分错，那么就会被“严重关注”，也就被赋上一个很高的权重。然后进行N次迭代（由用户指定），将会得到N个简单的分类器（basic learner），然后我们将它们组合起来（比如说可以对它们进行加权、或者让它们进行投票等），得到一个最终的模型。

原始的Boost算法是在算法开始的时候，为每一个样本赋上一个权重值，初始的时候，大家都是一样重要的。在每一步训练中得到的模型，会使得数据点的估计有对有错，我们就在每一步结束后，增加分错的点的权重，减少分对的点的权重，这样使得某些点如果老是被分错，那么就会被“严重关注”，也就被赋上一个很高的权重。然后等进行了N次迭代（由用户指定），将会得到N个简单的分类器（basic learner），然后我们将它们组合起来（比如说可以对它们进行加权、或者让它们进行投票等），得到一个最终的模型。

而Gradient Boost与传统的Boost的区别是，每一次的计算是为了减少上一次的残差(residual)，而为了消除残差，我们可以在残差减少的梯度(Gradient)方向上建立一个新的模型。所以说，在Gradient Boost中，每个新的模型的简历是为了使得之前模型的残差往梯度方向减少，与传统Boost对正确、错误的样本进行加权有着很大的区别。

具体的算法为：

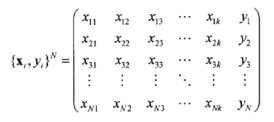
我们的目标是在样本空间上，找到最优的预测函数，使得X映射到y的损失函数达到最小，即：

损失函数的平方误差：

假设预测函数F(X)以P={P1,P2,…} 为参数，并可以写成若干个弱分类器相加的形式，其中P={    }, 第m个弱分类器的表达形式为，其中）表示第m棵回归树，向量表示第m棵回归树的参数，表示第m棵回归树在预测函数中的权重：

那么对于N个样本点，其优化问题等价于找到参数，m=0,1,2,…,M,使得：

求解归为以下迭代过程：

1.  首先定义初始化分类器为常数 ，其中表示初始化弱分类器，常数使得初始预测损失函数达到最小值：

2.  在每次迭代中都构造一个基于回归树的弱分类器，并设第m次迭代后得到的预测函数为（X），相应的预测函数为L(y,(X))

，为使预测损失函数减小得最快，第m个弱分类器应建立在前m-1次迭代生成的预测损失函数的梯度方向，其中（）表示第m次迭代的弱分类器的建立方向，

L(,())

表示前m-1次迭代生成的预测损失函数，表达式为L(,()) = 

基于求得的梯度下降方向，参数是使回归树沿此方向逼近的参数值，即：

是沿此方向搜索的最优步长，即：

3.  更新每次迭代后得到的预测函数，即

(x) = (x) + 

若相应的预测损失函数满足误差收敛条件或生成的回归树达到预设值M，则终止迭代。

4. 为避免过拟合现象，通常在每个弱分类器前乘上“学习速率”，值域为0～1，值越小，学习越保守，达到同样精度需要的迭代次数越大，反之，学习越快速，越容易出现过拟合：

值得一提的是，GBDT天然具有的优势是可以发现多种有区分性的特征以及特征组合。我们可以将GBDT和LR结合起来，具体如下：

先用已有特征训练GBDT模型，然后利用GBDT模型学习到的树来构造新特征，最后把这些新特征加入原有特征一起训练模型。构造的新特征向量是取值0/1的，向量的每个元素对应于GBDT模型中树的叶子结点。当一个样本点通过某棵树最终落在这棵树的一个叶子结点上，那么在新特征向量中这个叶子结点对应的元素值为1，而这棵树的其他叶子结点对应的元素值为0。新特征向量的长度等于GBDT模型里所有树包含的叶子结点数之和。

举例说明。下面的图中的两棵树是GBDT学习到的，第一棵树有3个叶子结点，而第二棵树有2个叶子节点。对于一个输入样本点x，如果它在第一棵树最后落在其中的第二个叶子结点，而在第二棵树里最后落在其中的第一个叶子结点。那么通过GBDT获得的新特征向量为[0, 1, 0, 1, 0]，其中向量中的前三位对应第一棵树的3个叶子结点，后两位对应第二棵树的2个叶子结点。

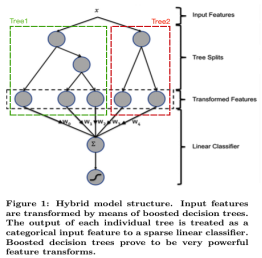
LR虽然简单，且训练预测效率高，但特征工程非常重要，现有的特征工程实验，主要集中在寻找到有区分度的特征、特征组合，折腾一圈未必会带来效果提升。GBDT算法的特点正好可以用来发掘有区分度的特征、特征组合，减少特征工程中人力成本。2014 Kaggle CTR竞赛冠军就是使用这种组合方法，笔者也是向他们学习。

References

1.  Xinran He et al. Practical Lessons from Predicting Clicks on Ads at Facebook, 2014. ↩